Hobart and William Smith Colleges

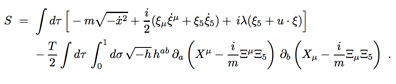
TED ALLEN, PROFESSOR

My research interests are in the general area of theoretical particle physics and gravitation. The two most prominent themes of my current research are QCD Strings and Constrained Quantization.

Quantum Chromodynamic Strings

Lattice calculations show that while the color force binding together a quark and an anti-quark behaves much like the electromagnetic force on very small scales, the color flux coalesces into a string-like object when the quark separation becomes appreciable on the nuclear scale. Mechanically, such a bound system acts like two point masses connected by a cord of energy. This cord, or string, can vibrate and the system can behave in more complicated and interesting ways than, say, a hydrogen atom. A while ago my collaborators and I found a model of this string and the quarks it connects that also incorporates the spin of the quarks. I am currently working to construct the quantum mechanics of this system.

Constrained Mechanical Systems and their Quantization

Most fundamental theories of physics have continuous symmetries that make their description of the physics redundant; they are constrained systems. The quantum mechanics of these systems must take these symmetries into account. I am interested in constructing new tools and applying existing tools to construct the quantum mechanics of constrained systems.

Other research interests of mine are the relationship between gravity, quantum mechanics, and thermodynamics; vortex dynamics and the fractional quantum Hall effect; potential models for quark confinement; and topological mass mechanisms.

Steve Penn, Associate Professor 

My research is in gravitational wave astrophysics. The potential for gravitational wave astrophysics is best summarized by a recent quote from the National Academy’s Decadal Survey on Astronomy and Astrophysics 2020.

"Gravitational wave astrophysics is one of the most exciting frontiers in science. One of the survey’s key priorities is the opening of new windows on the dynamic universe, with gravitational wave detection at the forefront. The continued growth in sensitivity of current-generation facilities, such as LIGO, through phased upgrades and planning the next-generation observatory, such as Cosmic Explorer, is essential. This will require investment in technology development now. The survey committee strongly endorses gravitational wave observations as central to many crucial science objectives." [Emphasis mine.]

Therefore, during these early years of Gravitational Wave Astrophysics, the fastest means to grow this field is by increasing the detector sensitivity, which increases the event rate and the SNR. For the LIGO detector, the most promising and practical path for maximizing its sensitiv- ity is through the reduction of 3 main noises sources: Suspension thermal noise, Laser quantum noise, and Coating thermal noise.

I was on the research team that first measured LIGO's Coating Thermal Noise. that determined the source of the noise, and that developed the mirror coating for Advanced LIGO (which detected gravitational waves).  My current research is on crystalline GaAs/AlGaAs mirror coatings that have 10x lower noise than the Advanced LIGO coatings.

DONALD SPECTOR, PROFESSOR

My research is multi-faceted, generally focusing particle theory and mathematical physics, with opportunities for involvement by interested students. Two current areas of my work that explore ideas relevant to quantum field theory and string theory are as follows:

• Developing a geometric characterization of shape invariance. Shape invariance is the principle underlying quantum systems that can be solved completely. Having previously showed that shape invariance is based on a BPS structure, an algebraic phenomenon known from the study of monopoles and strings, I am now aiming to use flux quantization to provide a geometrical formulation of the BPS interpretation of shape invariance, so that we know why this BPS structure appears.
• Is the Hagedorn temperature a fundamental limit? String theory appears to have a maximum possible temperature, termed the Hagedorn temperature. My work on number theory and supersymmetry has identified a whole class of additional models that also possess a Hagedorn temperature. In these models, I am examining whether this temperature is a fundamental physical limit or an artifact of the mathematical formulation. Preliminary evidence suggests that Hagedorn temperature might be an artifact that reflects the presence of a hidden sector of particles, whose interaction with ordinary matter only becomes relevant at high energies.

Other areas in which I have an interest include analog algorithms in quantum computing, cooling schedules in simulated annealing, the bosonic decay of Q-balls, the engineering of quantum potentials to produce logarithmic spectra, the use of first-order phase transitions to model phenomena in computer science, economics, and biology, and anything to do with supersymmetry.